Curvature Optimization 2D

Optimizing Radius of Curvature for Production and Printing

Kolkata, India

2018 - Ongoing

 Discretization of freeform curves into arc segments eases up the fabrication process in terms of cost, time and complexity. The following work is a starting of a research that aims at curvature optimization in curves and in surfaces and discretization into finite elements.

Experimental Setup:

The setup takes a free form curve and number of sample as input to process. Initially it samples the curve at certain parameter and check for the radius. If radius of curvature at that point is R ,then based on curvature  the curve is split at consecutive domain at value obtained from the following equation:

Further the curve is split at those points. The more the radius of curvature the less the interval of the splitting of the curve to adjust the span. At lower radius of curvature the splitting become more dense.

Segmented Arc approximation of curve

Implementation in Grasshopper:

The process has been implemented through GHPython Code in Node. It has used the basic ghpython.components library to implement. The same logic was establish using the native GH components to test the functionality but the python one runs faster due to implementation of parallel computing.

In 10 samples in a 42m span of curves the variation is found to be 51mm at maximum in the test curve.

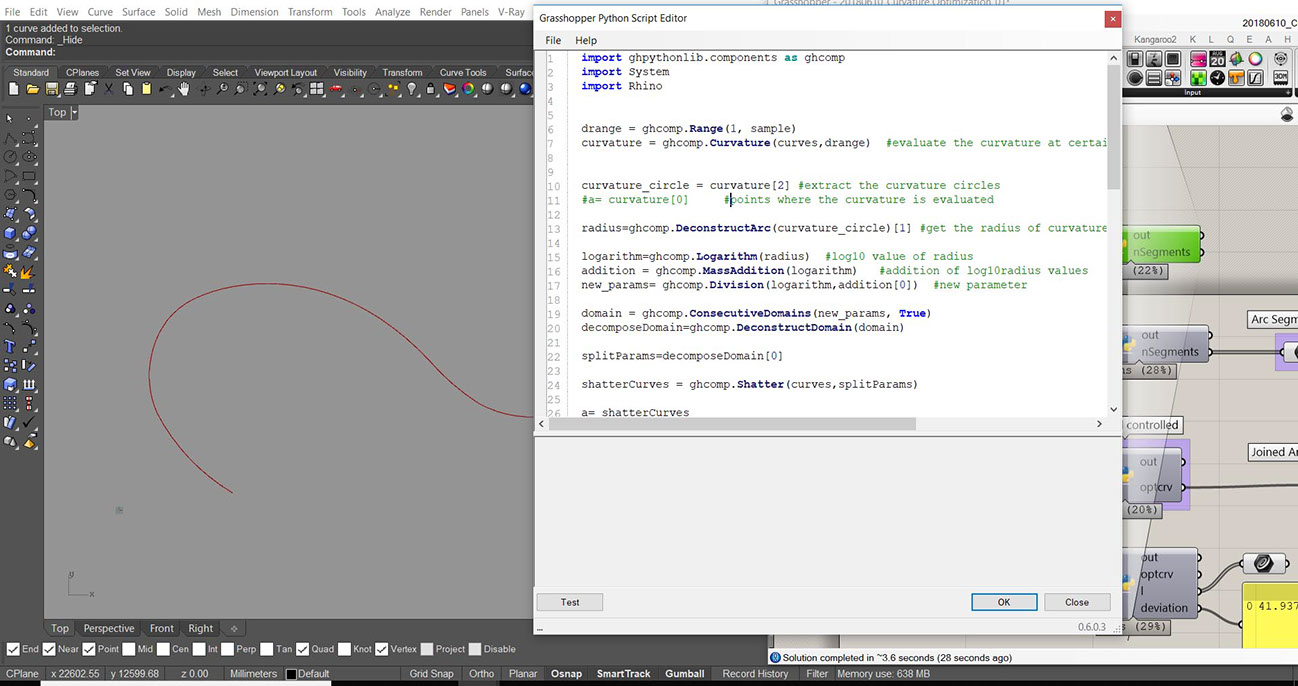
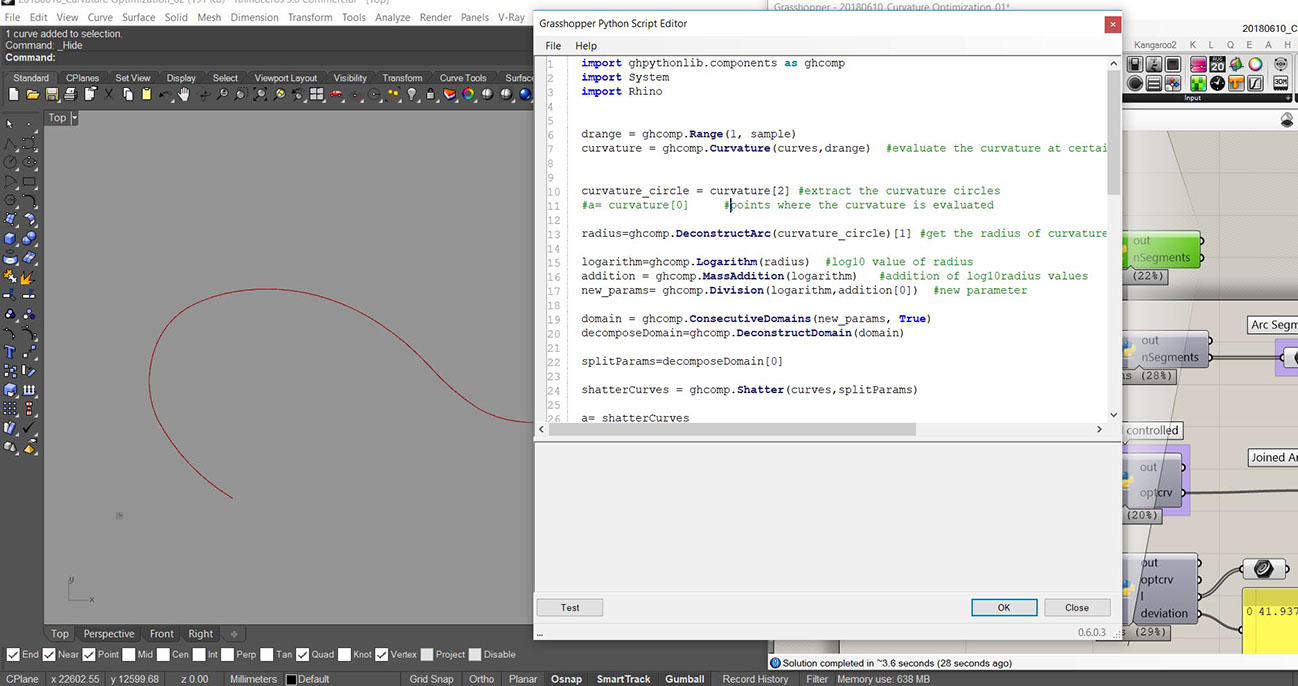
GHPython implementation | Rhino- Grasshopper